Modeling employee attrition and describing reasons why an employee might quit.
Exploratory Analysis
First, import the data and look at the structure of the variables. There are multiple factors coded as numerics, so I choose to change them all first, then call a summary on the data to get a high-level view of it.
data <- read.csv("/Users/vincentlee/Desktop/UGRID/UGRID2017/HR_analytics.csv")
str(data)
## 'data.frame': 14999 obs. of 10 variables:
## $ satisfaction_level : num 0.38 0.8 0.11 0.72 0.37 0.41 0.1 0.92 0.89 0.42 ...
## $ last_evaluation : num 0.53 0.86 0.88 0.87 0.52 0.5 0.77 0.85 1 0.53 ...
## $ number_project : int 2 5 7 5 2 2 6 5 5 2 ...
## $ average_montly_hours : int 157 262 272 223 159 153 247 259 224 142 ...
## $ time_spend_company : int 3 6 4 5 3 3 4 5 5 3 ...
## $ Work_accident : int 0 0 0 0 0 0 0 0 0 0 ...
## $ left : int 1 1 1 1 1 1 1 1 1 1 ...
## $ promotion_last_5years: int 0 0 0 0 0 0 0 0 0 0 ...
## $ sales : Factor w/ 10 levels "accounting","hr",..: 8 8 8 8 8 8 8 8 8 8 ...
## $ salary : Factor w/ 3 levels "high","low","medium": 2 3 3 2 2 2 2 2 2 2 ...
data[,3] <- as.factor(data[,3])
data[,5] <- as.factor(data[,5])
data[,6] <- as.factor(data[,6])
data[,7] <- as.factor(data[,7])
data[,8] <- as.factor(data[,8])
str(data)
## 'data.frame': 14999 obs. of 10 variables:
## $ satisfaction_level : num 0.38 0.8 0.11 0.72 0.37 0.41 0.1 0.92 0.89 0.42 ...
## $ last_evaluation : num 0.53 0.86 0.88 0.87 0.52 0.5 0.77 0.85 1 0.53 ...
## $ number_project : Factor w/ 6 levels "2","3","4","5",..: 1 4 6 4 1 1 5 4 4 1 ...
## $ average_montly_hours : int 157 262 272 223 159 153 247 259 224 142 ...
## $ time_spend_company : Factor w/ 8 levels "2","3","4","5",..: 2 5 3 4 2 2 3 4 4 2 ...
## $ Work_accident : Factor w/ 2 levels "0","1": 1 1 1 1 1 1 1 1 1 1 ...
## $ left : Factor w/ 2 levels "0","1": 2 2 2 2 2 2 2 2 2 2 ...
## $ promotion_last_5years: Factor w/ 2 levels "0","1": 1 1 1 1 1 1 1 1 1 1 ...
## $ sales : Factor w/ 10 levels "accounting","hr",..: 8 8 8 8 8 8 8 8 8 8 ...
## $ salary : Factor w/ 3 levels "high","low","medium": 2 3 3 2 2 2 2 2 2 2 ...
summary(data)
## satisfaction_level last_evaluation number_project average_montly_hours
## Min. :0.0900 Min. :0.3600 2:2388 Min. : 96.0
## 1st Qu.:0.4400 1st Qu.:0.5600 3:4055 1st Qu.:156.0
## Median :0.6400 Median :0.7200 4:4365 Median :200.0
## Mean :0.6128 Mean :0.7161 5:2761 Mean :201.1
## 3rd Qu.:0.8200 3rd Qu.:0.8700 6:1174 3rd Qu.:245.0
## Max. :1.0000 Max. :1.0000 7: 256 Max. :310.0
##
## time_spend_company Work_accident left promotion_last_5years
## 3 :6443 0:12830 0:11428 0:14680
## 2 :3244 1: 2169 1: 3571 1: 319
## 4 :2557
## 5 :1473
## 6 : 718
## 10 : 214
## (Other): 350
## sales salary
## sales :4140 high :1237
## technical :2720 low :7316
## support :2229 medium:6446
## IT :1227
## product_mng: 902
## marketing : 858
## (Other) :2923
There are no NAs, and no extreme outliers that suggest false data. Let’s continue by splitting the data between those who left and those who stayed, then comparing the summaries to get a sense of what might differentiate the employees who quit.
library(dplyr)
left <- subset(data, left == 1)
stay <- subset(data, left == 0)
summary(left)
## satisfaction_level last_evaluation number_project average_montly_hours
## Min. :0.0900 Min. :0.4500 2:1567 Min. :126.0
## 1st Qu.:0.1300 1st Qu.:0.5200 3: 72 1st Qu.:146.0
## Median :0.4100 Median :0.7900 4: 409 Median :224.0
## Mean :0.4401 Mean :0.7181 5: 612 Mean :207.4
## 3rd Qu.:0.7300 3rd Qu.:0.9000 6: 655 3rd Qu.:262.0
## Max. :0.9200 Max. :1.0000 7: 256 Max. :310.0
##
## time_spend_company Work_accident left promotion_last_5years
## 3 :1586 0:3402 0: 0 0:3552
## 4 : 890 1: 169 1:3571 1: 19
## 5 : 833
## 6 : 209
## 2 : 53
## 7 : 0
## (Other): 0
## sales salary
## sales :1014 high : 82
## technical : 697 low :2172
## support : 555 medium:1317
## IT : 273
## hr : 215
## accounting: 204
## (Other) : 613
summary(stay)
## satisfaction_level last_evaluation number_project average_montly_hours
## Min. :0.1200 Min. :0.3600 2: 821 Min. : 96.0
## 1st Qu.:0.5400 1st Qu.:0.5800 3:3983 1st Qu.:162.0
## Median :0.6900 Median :0.7100 4:3956 Median :198.0
## Mean :0.6668 Mean :0.7155 5:2149 Mean :199.1
## 3rd Qu.:0.8400 3rd Qu.:0.8500 6: 519 3rd Qu.:238.0
## Max. :1.0000 Max. :1.0000 7: 0 Max. :287.0
##
## time_spend_company Work_accident left promotion_last_5years
## 3 :4857 0:9428 0:11428 0:11128
## 2 :3191 1:2000 1: 0 1: 300
## 4 :1667
## 5 : 640
## 6 : 509
## 10 : 214
## (Other): 350
## sales salary
## sales :3126 high :1155
## technical :2023 low :5144
## support :1674 medium:5129
## IT : 954
## product_mng: 704
## RandD : 666
## (Other) :2281
Some observations:
Those who left had higher monthly hours worked.
Very low level of promotions for those who left. Most high paid employees did not leave.
Those who left had a higher amount of work accidents and ~20% lower satisfaction.
High projects indicates more likely to leave - no one with 7 projects stayed. Since left had higher monthly hours worked, I made a plot to investigate the effect these hours have on the employee’s satisfaction level among those who left, also taking into account number of projects.
library(ggplot2)
ggplot(left, aes(x = average_montly_hours, y = satisfaction_level)) +
geom_jitter (aes(color = number_project)) +
labs(title = "Employee Satisfaction vs. Hours Worked", x = "Hours per Month", y = "Satisfaction Level")
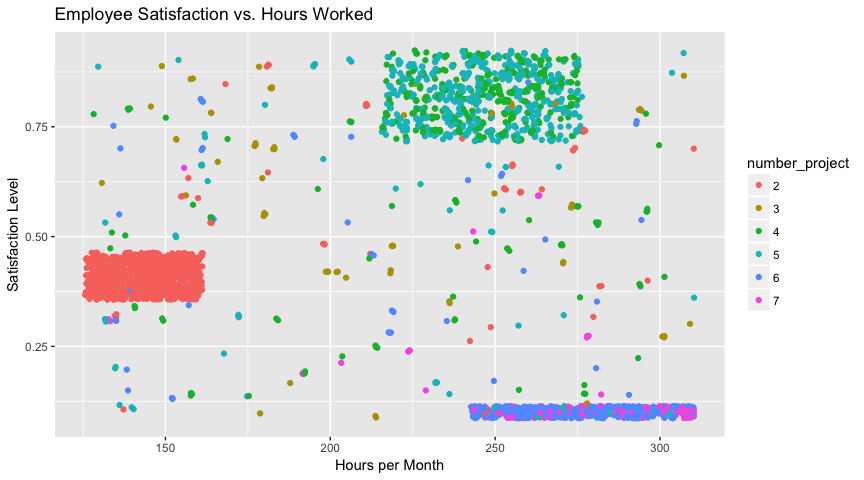
This plot indicates there are three main groups among the employees who quit: those who worked few hours per month and were moderately dissatisfied with their jobs, those who worked normal hours and were moderately-to-very satisfied with their jobs, and those who worked heavy hours who were very dissatisfied with their jobs. Don’t focus on the group that quit while they were satisfied - it is likely due to outside factors like spouse moving or outside promotion. Instead, make conditions better for unsatisfied workers, especially those with many projects and working more than 8 hours a day. Another potential relationship I wanted to explore was between an employee’s satisfaction level and their last evaluation score based on those who left.
ggplot(left, aes(x = last_evaluation, y = satisfaction_level)) + geom_jitter(aes(col = promotion_last_5years)) + labs(title = "Employee Satisfaction from Last Evaluation", x = "Last Evaluation Score", y = "Satisfaction Level")
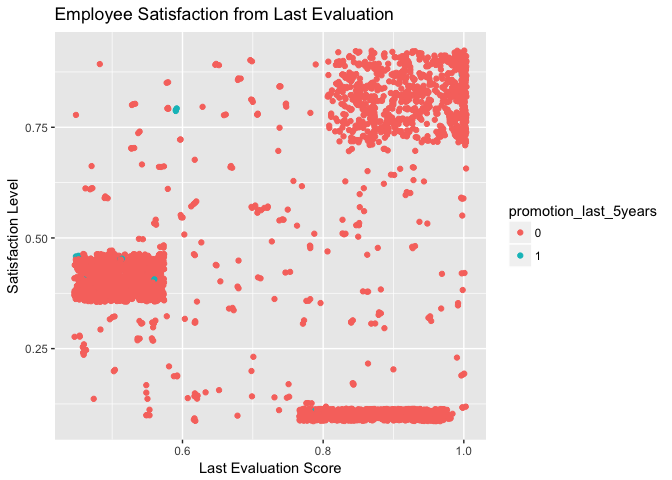
Interestingly, the same clusters emerge: this plot indicates that the same group who works fewer hours are the ones who score low on their evaluation; on the other hand, the ones who work normal-to-heavy schedules all recieved mostly positive evaluations, but are still strongly split between enjoying and hating their jobs. The company needs to avoid assigning people who are already working 9-10 hours a day with more projects in order to keep stress down and satisfaction up. The exceedingly low number of promotions among those who left is also clear in this plot, and perhaps more upward mobility would benefit the company’s employee retention rate.
Modeling
Finally, I wanted to create a model from the data to predict an employee’s satisfaction level. I decided to use linear regression for this task, but I think using logistic regression to predict the variable left could also work well. I started off with a model including all variables, then used stepwise elimination to determine which variables were the most significant towards predicting satisfaction.
modleft <- left[,-7]
mod <- lm(satisfaction_level ~., data = modleft)
step(mod)
mod <- lm(satisfaction_level ~ last_evaluation + number_project +
average_montly_hours + time_spend_company,
data = left)
summary(mod)
##
## Call:
## lm(formula = satisfaction_level ~ last_evaluation + number_project +
## average_montly_hours + time_spend_company, data = left)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.70806 -0.02640 0.00396 0.03314 0.70992
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.713e-01 2.453e-02 15.132 < 2e-16 ***
## last_evaluation 2.600e-01 2.287e-02 11.369 < 2e-16 ***
## number_project3 1.020e-01 1.634e-02 6.242 4.82e-10 ***
## number_project4 1.382e-01 1.314e-02 10.519 < 2e-16 ***
## number_project5 1.273e-01 1.323e-02 9.626 < 2e-16 ***
## number_project6 -2.906e-01 1.387e-02 -20.948 < 2e-16 ***
## number_project7 -3.048e-01 1.482e-02 -20.558 < 2e-16 ***
## average_montly_hours -3.932e-04 7.316e-05 -5.374 8.18e-08 ***
## time_spend_company3 -3.717e-02 1.782e-02 -2.086 0.0371 *
## time_spend_company4 -9.925e-02 1.625e-02 -6.109 1.11e-09 ***
## time_spend_company5 1.327e-01 1.583e-02 8.386 < 2e-16 ***
## time_spend_company6 1.611e-01 1.713e-02 9.401 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1071 on 3559 degrees of freedom
## Multiple R-squared: 0.8358, Adjusted R-squared: 0.8353
## F-statistic: 1646 on 11 and 3559 DF, p-value: < 2.2e-16
anova(mod)
## Analysis of Variance Table
##
## Response: satisfaction_level
## Df Sum Sq Mean Sq F value Pr(>F)
## last_evaluation 1 8.264 8.264 720.122 < 2.2e-16 ***
## number_project 5 187.598 37.520 3269.331 < 2.2e-16 ***
## average_montly_hours 1 0.584 0.584 50.881 1.184e-12 ***
## time_spend_company 4 11.399 2.850 248.314 < 2.2e-16 ***
## Residuals 3559 40.844 0.011
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
The model’s parameters confirm the suspicion that higher number of projects and monthly hours decrease employee satisfaction, and also imply that scoring higher on the last evaluation and loner time spent indicate higher satisfaction, which makes sense. The ANOVA indicates that number of projects and time spent have the highest impact on an employee’s happiness. The model also has a fairly high adjusted R-squared of 0.835, which is much higher than the values when the same model is trained on the stayed (or general) dataset. For some basic diagnostics using ggplot:
library(ggfortify)
autoplot(mod)
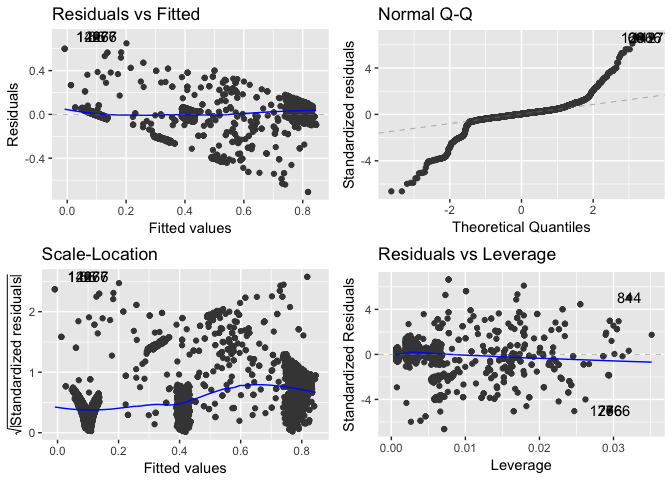
The residuals vs. fitted plot shows that the residuals follow a roughly linear pattern. The Q-Q plot shows the residuals are normally-distributed towards the center, but taper off at the beginning and end. This could potentially be addressed with the use of a transformation term. The scale-location plot shows the model’s lack of equal variance, mostly caused by the three large clusters. The residuals vs. leverage plot shows that no outliers especially affected the model. We can do some basic model fitting to see how well it works to predict the training set.
actual_scores <- left[,1]
pred <- predict(mod, left[,-1], interval="predict")
mse.train <- mean((pred - actual_scores)^2)
mse.train
## [1] 0.04094686
A MSE of only ~0.04% shows that the model can indeed predict the values it has been trained on well, but how about a more general set of data? We can’t use the exact same model because of some missing factor variables in the left subset, but if we retrain the model on all of the data and try another test…
mod <- lm(satisfaction_level ~ last_evaluation + number_project +
average_montly_hours + time_spend_company,
data = data)
actual_scores <- data[,1]
pred <- predict(mod, data[,-1], interval="predict")
mse.test <- mean((pred - actual_scores)^2)
mse.test
## [1] 0.1426782
It’s clear the model doesn’t work as well on the more generalized set of data, with a .10 higher MSE.
Conclusions and Next Steps
ggplot(data, aes(x = time_spend_company, y = average_montly_hours, col = left)) + geom_jitter() + labs(title = "Time Spent at Company vs. Average Hours Worked", x = "Years at company", y = "Monthly hours worked")
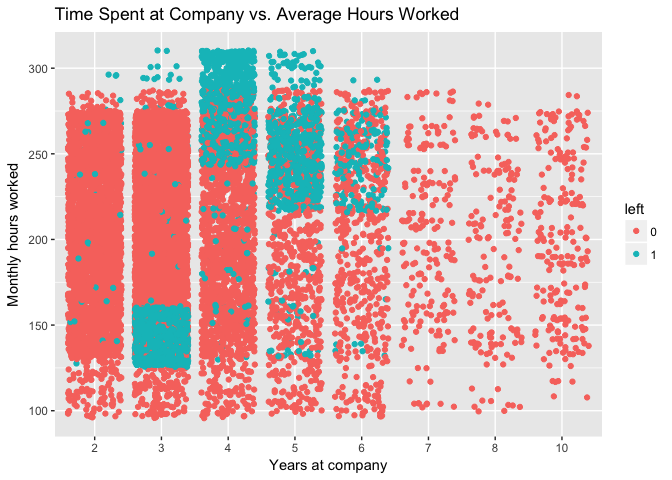
The main cause of employee churn seems to be caused by too many projects being assigned to those already working more than the average amount per week. Spread these out among those who work the least and have the least amount of projects. Try to focus on those who have been working for 3-5 years since the data indicates that these groups are the most likely to quit and the longer an employee stays, the more satisfied and less likely to quit they are.
More advanced modeling could be done to try to predict employee satisfaction or churn. K-means clustering and random forest algorithms could be used to attempt to describe the data. More analysis could also be done into how salary and department may affect churn. Outside variables like how long employees stayed before leaving and more info about their personal lives could help us make better models and more interesting associations among variables.